Last week i was watching a documentary that i wanted to see for some time. it is about this documentary from BBC, story of maths . If you didn’t see it, i recommend it to you.
The documentary has 4 parts, and i believe that in the first part, “The Language of the Universe”, i saw an interesting problem from the time of babylonians.
Like the most math problems of the time is about areas; the modern math has it’s roots to the desire of man to be able to calculate and store information about distances, surfaces and patterns.
Archaeologists found pieces of clay with inscriptions that are believed to be children homework, one of them captivated my attention, it was something like this, ( please excuse my lack of talent for graphic art ) :
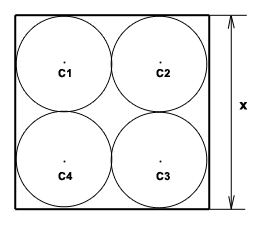
Let say we have a square with four circles inside it ( equal radius circles ), all circles are tangent to the square and to one each other. The square has a given length of it sides, let say x, for algebraic purpose.
The question is, what is the area of one circle ?
You will say, “what is so hard ?
We know the length of the square’s side ( x = any pozitive real number ), so we can extrapolate the circle radius ( r = one circle radius), and then calculate the surface of the circle.” … simple, huh ?!
r = x / 4
Scirc = πr2 = π(x / 4)2 = πx2 / 16 , for a discrete value, let’s say x = 5, Scirc = π52 / 16 = 0.5625 * π
The fun part is that the ancient babylonians did not have a precise method to calculate the surface of a circle, this was done by considering the circle a polygon with “many” sides.
Other method is to calculate the area of the square, and then subtract the area of the shapes between the circles and the square’s sides ( approximating those to known geometric figures, 8 triangles and a square ), and divide the result by four … quite laborious and not so precise.
Leave a Reply